Overgrowth, Pruning and Infantile Amnesia

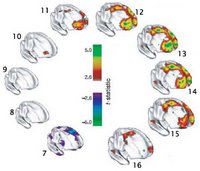
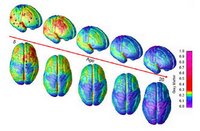As discussed yesterday, the current issue of Nature contains an article showing that the smartest children are those whose cortical thickness follows a specific trajectory, of initial thickening and then rapid thinning. These processes are hypothesized to map on to a period of myelination and then of pruning, but the exact mechanisms are unknown.

Can computational modeling provide any insights into what patterns of myelination and pruning are most effective? One clue comes from a study by Meilijson and Ruppin in a 1998 issue of Neural Computation. The authors show that to maximize the network's signal to noise ratio, and assuming that there is some upper metabolic constraint on neural processing (modeled as limited total number of synapses), synaptic pruning is effective if one follows a "minimal value" function, in which one deletes all synapses with magnitude below some threshold and leaves all others intact. On the other hand, if one assumes that the upper metabolic constraint is the total amount of synaptic efficacy that can be distributed through the network, a "compressing deletion" pruning strategy is best, in which the all synapses with efficacy above some threshold are reduced by a constant amount, and then all others are deleted. The authors describe that both probably apply in the brain, in which the relative importance of each constraint may determine which actual pruning strategy is used. This likely also differs between brain regions.

The authors' crucial finding is that given these metabolic constraints, the best pruning strategy is actually advantageous as compared to a fully connected "infant" network. In other words, an optimally pruned network will have more neurons than an unpruned network, although they both have roughly the same number of synapses or amount of synaptic efficacy. In the authors' own words, "the conclusion is that an organism that first overgrows synapses in a large network and then judiciously prunes them can store many more memories than another adult organism that uses the same synaptic resources but settles for the adult synaptic density in infancy."

Although the metabolic efficiency is improved, this comes at a price, as discovered by the authors in simulating pruning in the midst of learning (just as actually occurs in childhood). Adult networks that undergo synaptic pruning actually lose the ability to retrieve the earliest memories. In humans, this phenomenon is known as "childhood amnesia," in which memories before the age of 5 are hazy, and those before 3 are almost completely inaccessible. This amnesia emerges from the networks because the earliest memories are stored in a highly distributed fashion, relying on many different neurons, while later memories are stored in a more sparse format. Therefore, early memories are more degraded by the pruning strategy because of sheer probability: more neurons participate in their representation, so they are more easily affected by changes to the network.

These computational models provide a fascinating insight into the developmental trends discussed yesterday. Is it possible that the smartest children, whose cortex goes from relatively thin, to maximally thick, and then back again to relatively thin, would actually show less infantile amnesia than their mid-intelligence peers, whose cortices are initially thicker? If so, one wonders whether this might be causal as opposed to merely correlational with increased IQ measures, although this is purely speculative.

In botany, pruning induces "rejuvenation" at the pruned nodes. Perhaps neural pruning results in an overall decrease in cortical thickness, which is equivalent to why pruned plants will receive more sunlight, and yet also increases the efficacy of existing circuits, in the same way that pruned plants will yield more flowers and fruit. The metaphor is of course purely anecdotal, but one wonders whether these similarities might be more than mere coincidence.

This study has several broad implications for the field of artificial intelligence in general. First, should we limit the total number of synaptic connections/total amount of synaptic efficacy, to plausibly simulate biological metabolic energy consumption constraints? Second, given that an optimally pruned network is superior to all other networks with an equivalent number of synapses, and given that current computing power can only support some non-infinite number of synapses, should we simulate pruning in order to increase the effectiveness of machine learning?

Finally, is it possible to further increase network efficiency through recursively overgrowing and then pruning synaptic connections? There is some evidence that such recursive processes may occur in humans, as well; Jay Giedd discovered "a second wave" of neural overgrowth during puberty, which is followed by a second pruning process.

Related Posts:
The Structural Signature of Intelligence
Tuned and Pruned: Synaesthesia
Modeling Neurogenesis

The Structural Signature of Intelligence

A fascinating series of articles in today's issue of Nature documents work by NIMH researchers using MRI imaging to track structural changes in cortical thickness. Although one cannot predict IQ in adults or childen on the basis of cortical mass or thickness alone, the developmental trajectory of thickness changes are significantly related to IQ, such that those with the highest IQs (121-145) show an initial reliatively thin cortex, which rapidly thickens, and then thins again by 11 or 12 years of age.

"Brainy children are not cleverer solely by virtue of having more or less gray matter at any one age. Rather, IQ is related to the dynamics of cortex maturation,” said Rappoport, one of the authors on the study. A similar sentiment was expressed by Shaw, the lead author: "The story of intelligence is in the trajectory of brain development.” This relationship was strongest for prefrontal cortex thickness, which is often thought to be the seat of planning, strategizing, and other "executive functions." Although many previous studies attempting to relate IQ to brain structure were cross-sectional, this longitudinal study better controls for individual variation by following the same 307 subjects betweeen the ages of 5 and 19. They estimated IQ with subscales of the WAIS IQ test.

As Steven Rose points out (whose recent book was quite good), the IQ approach taken by these authors does not allow for direct causal ties between specific cognitive abilities and neural structure. Everything from emotional skills to recall ability may have some role in these net measures of IQ used here, and therefore it's difficult to tie this structural data to a cognitive level. More specific cognitive measures would have been helpful for interpreting the results of a a study this size.

A similar problem is that this research does not bear on the underlying mechanisms that give rise to this relationship between structure and IQ; it is purely descriptive. One parsimonious possibility, which is certainly supported by data, is simply that the smartest people are those with the most plasticity: indeed, those with superior intelligence show the most rapid thinning and the most rapid thickening of the cortex. As it turns out, IQ is significantly related to the speed of stroke recovery, which provides converging evidence for this hypothesis.

A second, related possibility is that the thickening stage is driven by myelination, a developmental process involving the encasement of neurons in white tissue which increases electrical conductance. Experience dependent pruning may also be involved in the cortical thinning trends observed.

Although it is tempting to attribute these complex developmental trends directly to genetic influences, this conclusion is premature and is even likely to be inaccurate. The relationship between gene expression and IQ is heavily modulated both by complex patterns of protein expression and interactions with the environment. For example, cortical thickness in rats is affected by the relative richness of their environment; in macaques, hippocampal neurogenesis only occurs in the absence of stress; likewise, as commentator Richard Passingham points out, changes in human cortical thickness could even be a result of practice. Or, it could simply be that more intelligent children are more likely to live in enriched environments.

Perhaps the strangest feature of this data is that IQ and cortical thickness have an initially negative relationship in the smartest subjects, which turns into a positive relationship as childhood progresses. A series of beautiful images in nature documents this reversal, one of which is included at the start of this article, shows the correlation between thickness change and IQ at each age.

Review: The Three Pound Enigma

How does "the mind" emerge from the brain? We are closer to a coherent answer than ever before, thanks to accumulating evidence from a variety of fields - including cognitive neuroscience, clinical psychology, internal medicine, somnology, and even modern philosophy. In "The Three Pound Enigma", Shannon Moffett explores the cutting-edge of these disciplines, literally: from the risky operation by neurosurgeon Roberta Glick described in the first chapter, to penetrating theoretical discussions with the sharpest researchers around (including vision scientist Christof Koch and philosopher Daniel Dennett), this book provides a cross-section of current brain research.

Unlike so many popular science books, "The Three Pound Enigma" has something for novices and experts alike. Clear explanations of everything from fMRI technology & K-complexes to anterograde amnesia & dissociative identity disorders will dazzle the layperson, and yet Moffett also provides something for the professional audience: a glimpse into the personalities of some of the field's most successful scholars, sufficiently detailed to give additional insight on their (in)famous theoretical perspectives.

For example, although many can lay claim to having late-night conversations about consciousness, very few (other than Moffett, and her readers) have had such a conversation in a crowded Memphis nightclub with renowned consciousness philosopher Daniel Dennett. Or, perhaps a better example may be the anecdotes related by somnologist Robert Stickgold, who traces his career from undergraduate neurobiology research at Harvard, to a stint as a computer programmer, first on Wall Street ... and then in one of the country's preeminent sleep labs. Or, better yet, Moffett gives fascinating context to one of the most unlikely collaborations in modern neuroscience: that between red-haired iconoclast Christof Koch and the late Francis Crick, a 1962 Nobel Laureate and the co-discoverer of DNA's double-helix structure.

Between clever quips (e.g., cognitive neuroscience: the expensive branch of philosophy) and penetrating insights about the current state of brain research, Moffett also includes "interludes," each of which documents a different stage in cognitive development, from conception to death. Although these sections are not tightly integrated with the text, they're useful grounding for both neuro-novices and experts alike. There's even a good deal of freely available web content, available for those who want to delve a little deeper into the topics discussed in the book.

In summary, Shannon Moffett's book is a wonderful introduction to the ideas underlying modern brain research, as well as a revealing portrait of several of the individuals driving these developments. The book comes highly recommended to laypeople with an interest in learning more about major players in brain research, and even to more experienced readers who desire a more personal view of the biggest names in the field.

Related Posts:
Review: Everything Bad Is Good For You
Review: Future of the Brain

Profile: Mark Tilden

Mark Tilden is a roboticist recently recruited by Wowwee Toys; Wowwee shortly thereafter released the Robosapien and the Roboraptor, with which Mark Tilden was clearly involved. Prior to working in the toy business, however, Mark led quite a different life: as a physicist at the Defense Department's Los Alamos National Laboratories, he was responsible for building autonomous, distributed and parallel-processing robots. Mark also worked at NASA, where he seems to have been intimately involved in the design of the Mars rovers.

A dominant theme in Mark Tilden's robotics research is embodiment. Many of his robots don't possess a central microprocessor - instead, they rely entirely on the non-linear coupled oscillations of electrical activity between as few as 12 transistors, connected in parallel. These patterns drive activity in the sensor and motor layers, and are "constantly attempting phase lock synchronization among variable pulse trains," according to Tilden's 2003 article in Robotics and Autonomous Systems. [Sound familiar?]

There are several major advantages to this approach, all of which contribute to what Mark calls a high "performance to silicon" ratio. First, Mark's robots are inexpensive. Many of the parts necessary to build an autonomous, foraging ant-like robot can be found inside a Sony Walkman. Second, much less building time (and no programming, at least in the traditional sense) is required: Mark claims to have built more than 500 autonomous robots, at less than 40 hours each (40 or 50 of these robots currently function as Mark Tilden's full-time housecleaners).

Finally, his robots are adaptive; because their behavior emerges from a sub-symbolic, non-linear, bi-directional interaction between a "nervous net" and its environment, the patterns of electrical activity driving all behavior are extremely plastic to changing situations. As a result, some of Mark's "biobugs" are still capable of movement after their legs have been sharply bent (a change that would surely foil any traditional symbolic mobility system), and are in some cases resilient to damage to 80% of their parts. Mark writes that "the loads generated by the motors directly modified the oscillator processes so that each motor [becomes] its own inertia-damped sensor ... This reduces robot control electronics to almost nothing, and as Nv systems are automatically self-optimizing, no programming is required either."

Mark refers to this architecture as biomorphic, and clearly takes many cues from nature. For example, in this interview Mark talks about the problem of motivation: without an internal drive for food (or power, more generally speaking) his robots have little need to move. But once he implements an appropriate "survival gradient," such as phototaxis, relatively organized behavior emerges. Here are some videos of these paradoxically simple machines.

Perhaps the most interesting, and yet most cryptic aspect of Tilden's work is the role of memory. His biorobots do not have memory per se; instead, their architecture can cultivate multiple attractor states. In other words, the creatures can show multiple patterns of behavior, as though they had been memorized.

It's still a matter of debate whether "biorobotics" actually has anything to teach biology. In fact, this article is dedicated to this far-from-resolved debate. Approaches like Tilden's are valuable even if it's only for their imaginative quality. However, the ultimate contribution of physical non-linear computation, like Tilden's, is likely to be much greater.

Interviews with Mark Tilden:
About his Los Alamos biorobots
About the Robosapien, from November 2004
About his DARPA work, including nanoscale MEMS
An upcoming documentary on Mark Tilden

Related Posts:
Binding through Synchrony: Proof from Developmental Robotics
Military Robotics: The State of the Art of War
Emotional Robotics
Imitation vs Self-Awareness: The Mirror Test
Neurorobotics
Giving the Ghost a Machine
A Mind of Its Own: Wakamaru

Dopamine: Before the Law

Dopamine (DA) has been proposed to underlie the process of reward learning, and specifically to play a critical role in the flow of information through the thalamo-cortical loops joining prefrontal cortex and basal ganglia. As the logic goes, phasic dopamine bursts from the ventral tegmental area (VTA) trigger the "gating" of information into this working memory loop, based on experience with what information has been rewarding to maintain previously.

In the most recent issue of PNAS, authors Lodge and Grace ask what afferent signals prompt the phasic DA firing in the first place. They showed that tonic input from the laterodorsal tegmental nucleus (LDTg) actually allows the VTA dopamine neurons to fire when they receive excitatory activation. This leads to the somewhat confusing conclusion that the "gating" function by VTA has its own "gate," provided by LDTg.

In vivo, VTA DA neurons usually show an irregular firing pattern of around 4 Hz (with a range of 2-10 Hz). Interestingly, when LDTg is activated, it appears to increase the number of VTA neurons that are firing, but not their firing rate or their firing pattern. Instead, LDTg activation allows burst firing to take place; with an inactivated LDTg, VTA shows a very regular "pacemaker" patterns, the same as is normally observed in vitro (but has not been observed in vivo). The authors conclude that "disruption within the LDTg or in its regulation by the PFC could be an underlying factor in the pathophysiology of major psychiatric disorders."

As an aside, I have a feeling that this isn't the last "gating of gating" type function we'll see. The microcircuitry linking inhibitory interneurons and DA neurons is incredibly complex, and they maintain very sophisticated regulatory firing patterns. It sort of feels like Kafka's "Before the Law," in which there are doors upon doors (or gates upon gates?) through which we pass before we'll really understand the mechanisms driving intelligent behavior.

Related Posts:
Models of Dopamine in Prefrontal Cortex
Visualizing Working Memory
Task Switching in Prefrontal Cortex

Synchrony and "Perception's Shadow"

Some of the earliest solid evidence for direct involvement between synchronous neural firing and cognitive tasks comes from a 1999 Nature article by Rodriguez, George, Lachaux, Martinerie, Renault & Verela. Here the authors argue that cycles of desynchronization and then re-synchronization are an organizing principle of neural computation - they even imply that the stages of this cycle reflect the essential "information processing components" of cognition.

The authors presented ten subjects with images of faces, either upside down or upright; the stimuli used made the patterns appear essentially meaningless unless they were upright (for example, the picture at the start of this article is actually an upside-down face!). The authors performed a time frequency analysis of EEG activity while subjects were viewing these stimuli and pressing one of two keys to indicate whether they had seen a face.

Two gamma-activity peaks were induced by the stimuli: one 36 Hz peak at 230 ms post stimulus onset, with a second 40 Hz peak at 800 ms post stimulus onset. The first was significantly stronger in trials where faces were detected, while the second was somewhat stronger in trials where no faces were seen. Even more surprising, they found a complex pattern of synchronization and desynchronization but only in trials where faces were seen:

1) A significant increase in synchrony occured at 200-260ms after stimulus onset centered on left parieto-occipital and frontotemporal areas [this is thought to reflect perceptual processing]
2) This was followed by a marked relapse into asynchrony at 500 ms, at bilateral parietal and occipitotemporal areas [this is thought to "set the stage" for motor processing]
3) In both trial types, synchrony reemerged at around 700 ms (on average, and centered on right temporal and central regions.) [this is thought to reflect motor processing]

One finding which is particularly surprising is that the highest levels of gamma activity co-occurred with desynchronization (not synchronization, as is often assumed to be the case).

One cannot explain these results in terms of volume conduction, or spurious synchronization, because only 7% of the synchronous oscillations occurred between neighboring electrodes, and because phase-locking was significantly more prevalent in trials where faces were observed. Yeung et al. have pointed to methodological problems with studies that assume that phasic peaks in time-averaged EEG signals are the result of phase-synchronization between previously uncorrelated signals (they can just as easily be interpreted as phasic bursts of activity). This criticism does not apply to this study, because they performed trial-by-trial comparisons of phase differences between electrodes after wavelet analysis.

The authors conclude that these results suggest "that a transition between two distinct cognitive acts (such as face perception and motor response) should be punctuated by a transient stage of undoing the preceding synchrony and allowing for the emergence of a new ensemble, through cellular mechanisms that remain to be established."

It should be noted that this evidence is merely correlational, not causal, which is a criticism that is frequently leveled against arguments for the importance of synchrony. The best causal evidence for the involvement of synchrony comes from Burle, B. and Bonnet, M. (2000) "High-speed memory scanning: a
behavioral argument for a serial oscillatory model" which showed that one can decrease the efficacy of visual search processes by interfering with gamma-frequencies. Nonetheless, the study described above provides good evidence, in conjunction with research cited in previous posts (below) that "synchrony cycles" are a reliable part of successful cognitive processing.

Related Posts:
Entangled Oscillations
Anticipation and Synchronization
Gamma Synchrony

"Unbinding" Imagery Via Attention

Despite the lack of direct evidence on the relationship between attention and imagery, at least two broad claims are well supported: first, attention is required for the maintenance of imagery, and second, imagery loads more heavily on attention than does perceptual processing.

Imagery clearly requires the use of executive functions, including attention (e.g., mental rotation; Tarr, 1995), perhaps in the form of Logie’s (2003) “inner scribe.” Also, attention in imagery is similar to perceptual attention: for example, the inspection of imaginary detail takes both time and attention, just as the scrutiny of perceptual images does. Space-based attention also seems important for imagery, as suggested by the similarity of imagery scanning times with those found in equivalent perceptual scanning tasks (see Pylyshyn, 2003, for a skeptical summary of these results, although his explanations are inconsistent with data described in a previous post, Neural Codes for Perception and Imagery). Finally, the time to form a mental image is dependent on the number of parts it has (Pylyshyn, 2003), suggesting that attention may also be at least partly feature- or object-based in imagery tasks, as it is in pattern recognition.

Because imagery lacks the bottom-up support inherent to perceptual images, it may require increased top-down biasing by attention. One would suspect that with such strong biasing, imagery would be particularly vulnerable to disruption by perceptual inputs. Indeed, the presentation of visual noise disrupts the vividness of imagery (Baddeley & Andrade, cited by Logie, 2003) and the effectiveness of imagery-based mnemonics (Quinn & McConnell, 1996, cited by Logie, 2003). Interestingly, visual noise does not disrupt items already stored in working memory (Logie, 2003), suggesting that perceptual input has a targeted disruptive effect on attention but not working memory functions.

Related evidence comes from a patient described by Bartolomeo (2002) who displayed classic unilateral neglect while drawing a butterfly from memory (i.e., drawing only the wing on the right side). However, when asked to redraw the image with closed eyes, he was capable of drawing a complete butterfly! This evidence is consistent with the speculative framework outlined above, in which the increased attentional biasing involved in imagery is particularly vulnerable to visual input. To put it another way, this patient’s tendency to attend to the right hemifield (RH) created a positive feedback loop: resulting in increased drawing in the RH, resulting in increased bottom-up support and hence more attention to the RH, resulting in yet more drawing in the RH, etc. This is a beautiful demonstration of the vulnerability imagery has to perceptual input, as a result of strong attentional biasing.

In summary, the relationship of imagery to attention is in some ways analogous with the relationship of pattern recognition to attention: there’s evidence for both location-based as well as feature/object-based attention in imagery tasks. Imagery may load more heavily on attention to sustain itself because it lacks bottom-up input. Because imagery requires this increasing top-down biasing, interference from perceptual input may be amplified. This conjecture is supported by evidence from the “butterfly patient” and the influence of visual noise on imagery tasks, described above.

One fascinating, but as yet unsupported hypothesis is that attention may be required for the "unbinding" of representations in mental imagery. Remember that attention is required for "binding," in which the neural processing of various object characteristics are brought together into a single, unitary representation. As discussed previously, the flow of perceptual information is reversed in mental imagery: neural data goes from long term memory to primary visual areas, rather than the other way around. It may be that attention is required in the process of "decompressing" visual data from the representational format of long term memory, or in other words, the "unbinding" of the representation from long-term memory into a mental "image" that is supported by activity in primary visual areas.

Related Posts:
Neural Codes for Perception and Imagery
Dissociations between Perception and Imagery
An Information Processing Approach to Mental Imagery
Attention: The Selection Problem
The Binding Problem

References:

Bartolomeo P. (2002) The relationship between visual perception and visual mental imagery: a reappraisal of the neuropsychological evidence. Cortex. 2002 Jun;38(3):357-78.

Logie, RH (2003). Spatial and Visual Working Memory: A Mental Workspace. The Psychology of Learning and Motivation. Volume 42. Academic Press. 37-38

M. Tarr, (1995) "Rotating objects to recognize them: A case study of the roleof viewpoint dependency in the recognition of three-dimensional obejcts," Psychonomic Bull. Rev., vol. 2, no. 1, pp. 55--82, 1995.

Pylyshyn Z. (2003) Return of the mental image: are there really pictures in the brain? Trends Cogn Sci. 2003 Mar;7(3):113-118.

Multiple Causality in Developmental Disorders

Computational modeling can allow scientists to observe the behavioral effects of many different types of network failure. In many cases, one observes "multiple causality" (Thomas, 2003) in which multiple types of disruptions to the network will result in similar behavioral deficits. This observation is important not just for understanding computational models, but for applied clinical psychology as well.

For example, ADHD-like behavior may have multiple orthogonal sets of underlying causes; these causes may also be behaviorally indistinguishable from one another. Thomas refers to this as a heterogenous disorder, in contrast to something like Williams Syndrome (which is understood genetically and therefore appears to be a homogenous disorder). The problem arises when one treats a heterogenous disorder; because different mechanisms may be causing the same behavioral deficit, the effects of therapy may be unpredictable, or in some cases even counterproductive.

How then, can we tell a heterogenous disorder from a homogenous one? One obvious option is to get additional behavioral measures, preferably of a different type: one would expect to find greater similarity among homogenous disorders than hetergenous disorders. Unfortunately, Thomas showed that this is not necessarily the case. First, he implemented a network that was capable of learning past tense formation on the basis of a large language corpus, and identified 10 "homogenously disordered" networks that performed poorly on tests of overgeneralization (sleep-sleeped) for a single reason (they used localist as opposed to distributed coding). Next, he created 10 "heterogenous" networks that showed increased overgeneralization of past tense formation, but for different reasons: some networks suffered from localist as opposed to distributed representations; others used a slower learning rate parameter, while others were missing a hidden layer. As a group, the heterogenous networks did not differ significantly from networks that were homogenously impaired on 4 other measures of past tense formation (even using non-parametric tests).

Even if the average performance of heterogenous and homogenous groups on multiple behavioral measures is not different at a single point in time, one might expect that these groups would show different developmental trajectories. Again, Thomas shows that this is not necessarily the case; by comparing the "longitudinal performance" (across 5000 training sets) of the homogenous and heterogenous disordered networks, there was no significant difference between them on any of the behavioral measures in one study. In a second study, one behavioral measure showed a difference between the groups, but this was not the disorder's diagnostic measure.

However, all is not lost: Thomas showed that even if heterogenous and homogenous networks do not necessarily differ in mean behavioral scores, they do differ in the variability of those scores relative to one another, and the change in variability over time. Homogenous groups in fact show higher variability on the diagnostic measure than heterogenous groups, and show lower variability in the other measures than on the diagnostic measure. In addition, the variability of the homogenous group's measures decreases over time, whereas this trend is much less apparent in hetergenous group measures.

In an analysis of two groups of children, those with Williams syndrome and those with Word-Finding Difficulties (homogenous and heterogenous disorders, respectively), Thomas showed that these trends hold in real data as well.

Unfortunately, this study bears several caveats (several of which Thomas himself mentions). First, individual differences can confound these results. Second, differences in measurement error between groups can also contribute to variability. Third, the homogeneity of underlying disorders is unlikely to be so black-and-white in actual practice, and may actually be more graded.

But the largest limitation of this study is that diagnosing individuals on the basis of variability requires that you already have baseline variability measures for the homogenous and hetergenous groups. In other words, to diagnose an individual on the basis of his/her variability, you need to be able to compare his/her variability to the variability of the heterogenous and homogenous groups. Unfortunately, it is precisely this distinction between groups which doesn't currently exist for many disorders. Hypothetically speaking, one might use a classifier (such as a neural network, or a support vector machine) to separate those individuals manifesting the characteristics of homogenous disorders from those with heterogenous disorders, but this approach was not mentioned by Thomas and still involves the caveats mentioned above.

Reference:

Michael S.C. Thomas (2003) Multiple causality in developmental disorders: methodological implications from computational modelling. Developmental Science 6:5 (2003), pp 537–556

Military Robotics: The State of the Art of War

Although these stories have been covered individually, I think it's important to provide an overview of current military robotics applications; not to endorse, but rather to disseminate, this information. Here is the current state of the art of robotic war:

S.W.O.R.D.S.:

Recently, defense contractor Foster Miller has developed a versatile robotics platform called "Special Weapons Observation Reconnaissance Detection System." This phrase, but not its acronym, obscures the real intent of this project. This platform (pictured at the start of the article) is compatible with the DREAD weapons system, described below:

"Imagine a gun with no recoil, no sound, no heat, no gunpowder, no visible firing signature (muzzle flash), and no stoppages or jams of any kind. Now imagine that this gun could fire .308 caliber and .50 caliber metal projectiles accurately at up to 8,000 fps (feet-per-second), featured an infinitely variable/programmable cyclic rate-of-fire (as high as 120,000 rounds-per-minute), and were capable of laying down a 360-degree field of fire"). [...] unlike conventional weapons that deliver a bullet to the target in intervals of about 180 feet, the DREAD's rounds will arrive only 30 thousandths of an inch apart (1/32nd of an inch apart), thereby presenting substantially more mass to the target in much less time than previously possible. This mass can be delivered to the target in 10-round bursts, or the DREAD can be programmed to deliver as many rounds as you want, per trigger-pull. Of course, the operator can just as easily set the DREAD to fire on full-auto, with no burst limiter. On that setting, the number of projectiles sent down range per trigger-pull will rely on the operator’s trigger control. Even then, every round is still going right into the target. You see, the DREAD's not just accurate, it's also recoilless. No recoil. None. So, every "fired" round is going right where you aim it.

U.A.V.: via Edge of Vision
"A small company called Neural Robotics has produced a robotic mini-helicopter armed with a rapid-fire shotgun. Based on their low-cost AutoCopter, the UAV (unmanned aerial vehicle) uses neural network-based flight control algorithms to fly in either a self-stabilizing semi-autonomous mode controlled by a remote operator, or a fully-autonomous mode which can follow GPS waypoints. A video of the AutoCopter Gunship is available."

"The AutoCopter Gunship UCAV/UCAR can also be outfitted with a thermal/IR sight, giving the system day/night/all-weather capability, so the operator can engage the enemy in any conditions the AutoCopter can handle from a flight perspective, even in total darkness."
"The AutoCopter can reportedly fly forward at 60 mph, and sideways at 35 mph, and can handle sling loads in gusting winds without any problem(s)."

Big Dog:

One obvious problem for military applications is that most robots are capable of traversing only simple terrain. Enter the "packbot" by Foster Miller and Boston Dynamics, whose slogan is "The Leader in Lifelike Human Simulation":

"sensors for locomotion include joint position, joint force, ground contact, ground load, a laser gyroscope, and a stereo vision system. Other sensors focus on the internal state of BigDog, monitoring the hydraulic pressure, oil temperature, engine temperature, rpm, battery charge and others."

AFATDS (aka AFTADS):

Obviously, one of the great advantages for having an autonomous robotic infantry is that they are capable of coordinating information and executing tactical strategies with much greater precision and speed than traditional units. Enter Raytheon & General Dynamics' AFTADS, the Advanced Field Artillery Tactical Data System, which is a command AND control system ("C2") currently installed in "all U.S. Army echelons from weapons platoon to corps and in the Marine Corps from firing battery to Marine Expeditionary Forces. AFATDS is installed aboard the U.S. Navy LHA/LHD Class big deck amphibious ships to support Expeditionary Strike Groups (ESGs) for amphibious operations."

"It processes fire mission and other related information to coordinate and optimize the use of all fire support assets, including mortars, field artillery, cannon, missile, attack helicopters, air support, and naval gunfire. [...] During battle, AFATDS will provide up-to-date battlefield information, target analysis, and unit status, while coordinating target damage assessment and sensor operations."

AFTADS is capable of managing all aspects of warfighting, including the validation of targets, the management of weapon systems/munitions status, analysis of all fire support assets, automatically applying tactical guidance for targeting and attack, continuously prioritizing of high-value and high-payoff targets, fully automating weapon-to-target pairing, the set up and coordination of all communications, and automated mission coordination in conjunction with established or evolving doctrine, tactics, techniques, and procedures. [This information is paraphrased from the data sheet linked to above].

Just to give you some idea of the destructive power available here, consider "the Crusader," which is a weapons system that AFATDS is capable of managing. The Crusader "consists of the next generation self-propelled howitzer (SPH) and [..] provides unprecedented lethality based on system responsiveness and rate of fire. The entire fire control and ammunition handling system for both the howitzer and RSV is automated. [...] A multiple round simultaneous impact (MRSI) capability allows one Crusader to deliver 4 to 8 rounds on a target within four seconds in a surprise fire-for-effect mode. Increased survivability is achieved by an integrated defense system that includes stealth design, lighter-weight armor protection [...] and the ability to make rapid survivability moves using shoot and scoot tactics to avoid enemy counterfire. The Crusader has a 30-40 km range." 30 to 40 km !

Although I have not been able to find this particular fact on the web (probably for good reason), I know from a first-hand source who trains soldiers on AFTADS that it is fully capable of operating within a "closed-loop," in which humans are not part of the target detection, fire planning, and fire execution cycle.

But without humans, who does the moment-by-moment tactical and strategic planning? Read on.

B.I.C.A.:

DARPA (Defense Advanced Research Projects Agency) has recently announced this new initiative (along with other biomimicry-oriented initiatives, such as SWARM, aka Smart Warfighting Array of Reconfigurable Modules). Given the lavish funding for grant winners, this announcement has many cognitive neuroscientists falling over one another to get their applications in order.

"The goal of the Biologically-Inspired Cognitive Architectures Program via this BAA is to develop, implement and evaluate psychologically-based and neurobiologically-based theories, design principles, and architectures of human cognition. In a subsequent phase, the program has the ultimate goal of implementing computational models of human cognition that could eventually be used to simulate human behavior and approach human cognitive performance in a wide range of situations" (presumably, including war).

"Our goal is to create challenges problems relevant to military situations that will serve this program and others as cognitive simulations evolve. The set of problems must be progressively more challenging, must involve both embedded and non-embedded problems. “Embedded” refers to problems in which an embodied cognitive agent is situated within, and interacts with, a physical environment which, may or may not contain other cognitive agents." (Clearly, "other cognitive agents" is a term that may eventually include humans.)

Related Posts:
Emotional Robotics
Constraints and Optimality
Binding through Synchrony: Proof from Developmental Robotics
Giving the Ghost a Machine
Neurorobotics
A Mind of Its Own: Wakamaru
Imitation Vs Self Awarenss: The Mirror Test

Relevant Companies:
RoboticFX
ICOSYSTEMS
Neural Robotics
I-Robot (the Roomba manufacturer recently won a defense contract)
Foster Miller
General Dynamics Robotics Systems
Boston Dynamics Robotics

If you liked this, don't forget to digg it.

Neural Codes for Perception and Imagery

Mental imagery may seem like it's too abstract to test scientifically. However, this week's posts have reviewed cognitive neuroscience approaches to mental imagery, and how it may differ from perception, using information processing analyses as well as detailed case studies of neurological patients. Overall, it appears that we actually use the same neural mecahnisms for mental imagery as we do for everyday perception, even though there are some patients with selective damage to either perception or imagery (there is reason to doubt the validity of many of these cases, as discussed yesterday). Does evidence from brain imaging technology (fMRI, SPECT) support this conclusion?

Kosslyn and Thompson showed that under most conditions, one will observe neural activity in primary visual areas when subjects are asked to imagine a visual object. But according to Kosslyn & Thompson’s analysis, relatively simple, non-spatial mental imagery may actually fail to elicit PVA activity. This brings us to a representational issue: if this activity is truly absent (as opposed to immeasurably small), then what kinds of representations are activated in these cases?

Both Kosslyn and Pylyshyn (the two primary opponents in the "great imagery debate") posit that structural descriptions are the storage format of long-term memory. This means that long term memory encodes information into an amodal format, consisting of symbols and spatial relations between those symbols (e.g., above, below, to the left of). Where Kosslyn and Pylyshyn differ, in terms of this small part of the debate, is that Pylyshyn claims such amodal, symbolic codes are sufficient for all mental “imagery” tasks per se. Pylyshyn argues that many of the behavioral results that are consistent with a "pictures in the brain" explanation of mental imagery are actually "faked" by participants, because they believe that is what is expected of them (this problem is known as "demand characteristics" in the literature). Pylyshyn has shown that by altering the tasks in such a way as to remove all demand characteristics, participants show behavioral results that are consistent with his view of mental imagery, in which activation of knowledge in long term memory is sufficient for all "mental imagery" tasks.

However, one major flaw plagues Pylyshyn’s logic when it comes to the aforementioned brain imaging data: if long-term memory actually contains directly accessible, highly-detailed information about the visual world, why would subjects ever activate primary visual areas, as seen in fMRI studies of mental imagery? Such activation would be unnecessary because long-term memory would contain all the tacit knowledge necessary to “fake” the RTs.

Therefore, the most plausible explanation of PVA recruitment in highly-detailed imagery tasks is that subjects are incapable of directly interpreting the highly-detailed information residing in long-term memory, but must instead “decompress” it into a format consistent with that used in primary visual areas. (In contrast, long term memory can provide relatively simple, structural information, which suffices in some low-detail imagery tasks, without requiring the full recruitment of PVAs)

Importantly, this viewpoint is consistent with the observation that mental imagery appears to work only with the interpreted versions of visual stimuli (Chambers et al., 1985, cited by Logie, 2003). In other words, imagine that you are presented with an ambiguous line drawing (pictured at the beginning of the article), which is removed as soon as you have identified one interpretation of the drawing. If you are then asked to mentally image the drawing, you are unable to determine whether a second interpretation is possible. However, as soon as you are presented with the original drawing again, determining the second interpretation is easy. (In this case, the drawing can be either a duck or a rabbit).

To summarize, subjects are incapable of decompressing visual information from associative memory into a format that is semantically neutral; semantic interpretations are pre-associated with visual information in the representational format used by associative memory. As suggested by Kosslyn, the flow of information is reversed in imagery, relative to visual perception: long-term memories are activated, and the visual data associated with them is projected back to primary visual areas. However, this pattern of activity includes the semantic processing that was originally associated with the image. The image cannot be reinterpreted precisely because the interpretation is driving the imagery!

In conclusion, the representations used by pattern recognition and mental imagery differ in that perceptual input can be semantically reinterpreted, while mental imagery cannot; they also differ in that perceptual input requires the use of PVAs, while mental imagery only elicits PVA activity for detailed information. On the other hand, mental imagery and pattern recognition use many of the same information processing components, as illustrated by both the rarity of double dissociations and Kosslyn’s parsimonious architecture of high-level vision.

Dissociations Between Perception and Imagery

To what extent do mental imagery and visual perception rely on the same neural machinery? Although early data suggested that imagery and perception were not neurally dissociable (Farah, 2000), suggesting that they may rely on nearly identical information processing components in the brain (as discussed in yesterday's post), more recent cases have illustrated a variety of ways in which the two functions can be selectively impaired. For example, some patients are able to draw an object from memory, but moments later are unable to recognize their own drawing.

How would one diagnose a problem with imagery as distinct from a problem with visual perception, or "object knowledge" more generally? The approach used by Farah with patient RM was to administer a sentence verification task in which half the sentences required mental imagery. For example, "A grapefruit is larger than a cantaloupe" would require verification by RM. Since it's unlikely that long-term associative memory contains this type of detailed information, one would have to engage in some kind of mental visual comparison. The other sentences to which his responses were compared did not require imagery, such as "The US government functions under a two-party system." Pretesting on normal subjects was used to equate these two sentence types on difficulty. RM performed poorly on the imagery questions, but did well on all other sentence verifications.

RM also underwent tests to verify that his perceptual and visual abilities were still intact. RM could name objects in pictures, could copy drawings nearly perfectly, but refused to complete the part of the test in which he was required to copy a drawing from memory. Likewise, when tested for his recognition of colors, he performed nearly perfectly, but was unable to declare the typical color of objects from memory.

Patient HJA (Humphreys & Riddoch, 1987) shows the opposite pattern; if asked to draw an object from memory, HJA could complete a realistic drawing, but was unable to recognize these objects in real life or answer imagery questions (e.g., "which has more red in it, a plum or an eggplant?"). Interestingly, as the years wore on, HJA lost this ability too, suggesting that visual semantic memory may require maintainence, or continual input from the environment, to remain accessible. Patient MD (Bartolomeo, 1998) showed a similar pattern of dissociations, in that she was impaired at identifying visual objects, but was perfectly able to answer questions involving mental imagery. Furthermore, she was frustrated that the researchers kept asking questions about her imagery abilities, which she emphatically claimed were fine!

Although these stories are fun to tell and fascinating to imagine, three points justify skepticism of these reports:

• First, these dissociations could be caused by a “disconnection” syndrome, in which afferent perceptual inputs to a shared imagery/pattern recognition system would be selectively damaged without concomitant damage to its efferent inputs (Farah, 2000).
• Second, many of the patients also sustained fairly broad impairments (including optic aphasia, prosopagnosia, and pure alexia; Bartolomeo, 2002), so their behavioral results should be interpreted as reflecting imagery problems only with caution.
• Third, the majority of cases reported before 1988 support the idea that imagery and pattern recognition are served by the same regions (Bartolomeo, 2002) and are quite rare.

Kosslyn & Thompson were able to identify the precise conditions under which perceptual primary visual area (PVA) regions are activated by imagery (2003). Asking subjects to visualize high-resolution details, requesting that those mental images be non-spatial, and using high-resolution neuroimaging techniques were all associated with increased PVA activity, and could together explain most variation in the existing PVA-neuroimaging data. To summarize, imagery may be anatomically distinct from pattern recognition only insofar as it deals with spatial, or low-resolution images.

Therefore, an interesting question is whether those patients showing selective impairments of perception and not visual imagery actually sustained damage to regions prior to primary visual cortex, or if perhaps they showed individual differences in the degree to which they activate PVA for detailed imagery. Nonetheless, this data poses a problem for Kosslyn's information processing approach to mental imagery: just because it appears to us that the same anatomical regions would be capable of supporting both mental imagery and perception, we should not assume that this is the case. As structural imaging gains resolution (such as dtMRI) we should be able to determine whether the double dissociations observed by Bartolomeo are in fact "disconnection" syndromes, or whether Kosslyn's architecture truly needs revision.

One clear theoretical problem lingers, however. According to Kosslyn & Thompson’s analysis, relatively simple, non-spatial mental imagery may actually fail to elicit PVA activity. If this activity is truly absent (as opposed to immeasurably small), then what kinds of representations are activated? Tomorrow's post will address the differences in the representational format of imagery and perception (or lack thereof?), using evidence from visual illusion research.

Related Posts:
An Information Processing Approach to Mental Imagery

An Information Processing Approach to Mental Imagery

An intense debate has surrounded the relationship of pattern recognition and mental imagery for many years. This debate can be distilled into three related questions: first, what kinds of information processing might accomplish both pattern recognition and mental imagery? Second, to what extent are these functions located in distinct anatomical regions? Third, how is visual data actively represented, and does that differ between mental imagery and perception?

To tackle the first question, Kosslyn’s (1990) cognitive architecture posits that both imagery and pattern recognition can be supported by nearly identical information processing units. The only unique subsystem required by mental imagery is the “shape-shift” system, which can alter the perceived shape, location, or orientation of objects on the visual buffer, and may be capable of additional transformations (such as folding or rotation).

With the exception of this shape-shift subsystem, visual perception and mental imagery differ according to this information processing approach only in the dominant direction of data flow: this flow is reversed for imagery because pattern recognition is being driven by internally generated, as opposed to externally generated, patterns of neural activity.

In summary, then, the processes of pattern recognition and imagery appear very similar at an "information processing" level of analysis, as conducted by Kosslyn. However, this tight relationship between imagery and pattern recognition conflicts with more recent cognitive neuroscience evidence, which suggests that perception and imagery may use some very different mechanisms (and in some cases can be selectively impaired). In other words, some neuropsychological patients are unable to use mental imagery, but can yet perceive the visual world without problems. Yet other patients with visual agnosias are unable to name visually presented objects, but are still able to successfully imagine named items.

Tomorrow's post will review this neuropsychological evidence, the clever behavioral tests used to diagnose the patients, and the implications for the machinery supporting both perception and mental imagery.

Related Posts:
Dissociations between Imagery and Perception
Pictures in the Brain
An Informal Integration of Object Recognition Models
Kosslyn's Cognitive Architecture

Attention: The Selection Problem

The solution to the binding problem (discussed yesterday) contains a second, related problem: at what point in the pattern recognition process, and hence on what kinds of representations, does attention operate? This is also known as the "space-based" versus "object-based" attention debate (covered previously by Cognitive Daily).

Posner’s early spatial cueing experiments encouraged the view that attention selects stimuli on the basis of spatial location. The importance of spatial location to attention is also supported by evidence for enhanced stimulus processing in the vicinity of attended targets (Connor, et al., 1997, cited by Kanwisher & Wojciulik, 2000). Certainly, spatial information is important both for pattern recognition and attention.

One might claim that “pop out” phenomena indicate that attention can be guided by specific features, perhaps as identified in a pattern-recognition preprocessing subsystem, (Kosslyn, 1990). This conclusion is essentially correct, although it is complicated by unusual task-dependencies; for example, reaction time is not related to set size in the detection of the letter T from a display of L’s, but if each letter in the display is randomly reoriented, the “pop out” effect disappears. Based on a detailed analysis of this and other evidence, Wolfe & Horowitz (2004) identified a short list of features that are “undoubtedly” sufficient for the guidance of attention. They concluded that attention is also guided by at least some features.

Finally, persuasive evidence indicates that attention can be object-based, even in cases where the objects are superimposed (Kanwisher & Wojciulik, 2000) or occluded by other objects (Wolfe & Horowitz, 2004). Interestingly, while perceptual load increases target selection efficiency in object-based attention, the opposite relationship exists between cognitive load and target selection (Yi, et al., 2004, and De Fockert, et al., 2001, respectively, cited by Lavie, 2005). One might speculate that high perceptual load increases the efficiency of target object selection by more fully tapping the competition among “preattentive” representations, whereas high cognitive load may attentuate the top-down biasing of relevant features, and hence cause increased distractor object processing.

In summary, attention both influences and is influenced by the entire pattern recognition process, from low-level spatial information all the way up to integrated object representations. Attention can play two seemingly incongruous roles: it both groups patterns into unitary objects, and is able to select among those objects.

This stance is consistent with Duncan’s (2005) definition of attention as a “ubiquitous, temporally extended” competition between representations, in which more currently-relevant representations are more strongly amplified. In addition, any bottom-up representation with high TD differences also strongly influences the deployment of attention. This dual perspective firmly situates attention at the end of a two-way street, in which it can both flexibly bias pattern recognition processes in a top-down fashion, and yet can also be strongly influenced by bottom-up representations.

Related Posts:
The Binding Problem
Selection Efficiency and Inhibition

References:

Duncan, J. (2005). EPS Mid-Career Award 2004: Brain mechanisms of attention. THE QUARTERLY JOURNAL OF EXPERIMENTAL PSYCHOLOGY. 2006, 59 (1), 2–27

Kanwisher N, Wojciulik E.(2000) Visual attention: insights from brain imaging. Nat Rev Neurosci. 2000 Nov;1(2):91-100.

Kosslyn SM, Flynn RA, Amsterdam JB, Wang G. Components of high-level vision: a cognitive neuroscience analysis and accounts of neurological syndromes. Cognition. 1990 Mar;34(3):203-77.

Lavie, N. (2005) Distracted and confused?: selective attention under load. Trends in Cognitive Sciences, 9, 75-82

Wolfe, JM & Horowitz TS. (2004). What attributes guide the deployment of visual attention and how do they do it? Nature Reviews Neuroscience, Jun;5(6):495-501

The Binding Problem

The "binding problem" refers to the fact that we experience the world as consisting of unitary objects, and yet all the information pertaining to any specific object is processed within vastly different regions of cortex. How does the brain know how to integrate the correct features into our experience of each object? Attention has been proposed in multiple theories (Treisman & Gelade, 1980; Wolfe, 1994) to be a kind of “glue” which integrates these anatomically distinct pattern activations into unitary objects representations.

One such theory of attention, Treisman’s Feature Integration Theory (FIT), posits preattentive and parallel feature detection, with serial deployments of attention binding these features into object files on a master “activity map.” Any stimuli falling within the focus of attention can be processed in parallel (i.e., the “group scanning hypothesis,” Quinlan, 2003).

Although initially too simplistic to account for behavioral data showing flat-response times for conjunctive searches (Quinlan, 2003), and despite subsequently detailed elaboration (e.g., “group scanning hypothesis,” and Wolfe’s related but distinct Guided Search model), several aspects of this attention/pattern-recognition relationship remain unsatisfactory.

First, the “glue” metaphor of attention does not always clearly relate to the biology of pattern recognition. For example, one might expect the features that cause “pop out” to map cleanly onto primary visual areas (PVA), but they do not: e.g., attention is required to discriminate oriented lines differing by less than 5˚, even though cells in V1 can reliably differentiate them (Wolfe, 2003).

Wolfe & Horowitz (2004) explained this difference as a function of signal-to-noise ratio, or alternately, target to distractor difference (TD). According to this view, “pop out” tasks are those manifesting a very large TD difference, and hence guide attention to the target almost immediately, whereas targets with a lower TD difference generally require longer to be detected. This viewpoint accurately portrays attention as sensitive to pattern heterogeneity.

However, the relationship between attention and pattern recognition described above contains a second, related problem: at what point in the pattern recognition process, and hence on what kinds of representations, does attention operate? This question will be reviewed in detail in upcoming posts.

Related Posts:
Binding through Synchrony: Proof from Developmental Robotics

References:

Treisman, A., Gelade, G. (1980) A feature-integration theory of attention. Cognitive Psychology, 1980 Jan;12(1):97-136.

Wolfe, J.M. (1994) Guided Search 2.0: A Revised Model of Visual Search. Psychonomic Bulletin & Review, 1(2): 202-238

Wolfe JM. (2003) Moving towards solutions to some enduring controversies in visual search. Trends Cogn Sci. 2003 Feb;7(2):70-76.

Wolfe, JM & Horowitz TS. (2004). What attributes guide the deployment of visual attention and how do they do it? Nature Reviews Neuroscience, Jun;5(6):495-501

Quinlan PT. (2004). Visual feature integration theory: past, present, and future. Psychol Bull. 2003 Sep;129(5):643-73

Visualizing Working Memory

Shiffrin's modal model of memory includes three parts: a brief sensory store through which we experience the outside world, a working memory component with rehearsal processes, and a long-term store from which we can retrieve information into working memory. (If you haven't seen it before, please view the classic model before reading on.) Although hugely influential, the model has a few unfortunate shortcomings.

Most importantly, memory is not a static process. Memory decays unless it follows the cycle of learning, encoding, recall, and recoding. In contrast, the classic "modal" model distinguishes storage functions from processing functions - i.e., one is a "black box" and one is a "black arrow." Unfortunately, this distinction is artificial, because the brain contains only arrows: processing (activation) and memory (synaptic efficacy) are two sides of the same coin, and memory itself is a process.

Second, all arrows are not created equal. "Architectural" differences (such as the synaptic efficacy of recurrent connections) among different parts of the brain lead to different processing profiles. These profiles can differ in terms of bandwidth, or in other words, how much information they are capable of holding at a time. Orthogonal to bandwidth, these profiles can also differ in terms of decay rate (or alternately, vulnerability to interference): that is, some regions are capable of maintaining information indefinitely while others are capable of maintaining memories for less than one second.

Third, multiple processing paths require gating functions. Perhaps the largest advantage of removing the "boxes" from the traditional "box and arrow" diagram is that one must become explicit about the functions performed at every step. As a result, such diagrams will be more likely to provide a nice one-to-one relationship between cognitive functions and neuroanatomy. And pure-arrow diagrams remove the need for some elusive "executive functioning" box to coordinate and configure the processes; instead, one need only posit a gating function at the intersection of every arrow with another, in which some process allows information to pass along from one arrow to the next (probably based on dopamine fluctuations).

Accordingly, my new visualization of the modal model uses only arrows, and two simple visual metaphors. First, those arrows with a wider base represent increased bandwidth or initial capacity. Second, the change of the width of each arrow as it moves through space represents the rate of decay. Finally, at the intersection of each arrow, a simple gating function allows memory to pass through from one or more of the receiving paths. In the rest of this post, I'll narrate the flow of information through this structure.

Sensory Memory. As you can see from the image at the start of the article, incoming sensory information has an extremely high initial bandwidth, and a rapid rate of decay, as indicated by the fat, short arrows. Furthermore, there is no rehearsal process, and sensory memory is constantly overwriting itself. This is indicated visually by the multiple arrows which overlap, and quickly diminish in width.

Working Memory. From sensory memory, perceptual data feeds into (or is "sampled" by) a relatively low-capacity - and low-decay - polymodal short-term/working memory process, as indicated by convergence of sensory inputs into an arrow of smaller width in the middle-lower region of the diagram. Importantly, the width of this arrow does not shrink over time, indicating that the rate of decay is extremely low; indeed, we can hold somewhere between 4 and 7 items in working memory (depending on modality) without decay. This short-term/working memory process feeds two unique rehearsal processes (each is robust to decay and yet limited in bandwidth).

These rehearsal "loops" are capable of refreshing short-term/working memory with previous information. The phonological loop is capable of maintaining verbal information, and the "inner scribe" supports imagery functions (such as mental rotation). Oscillatory cycling of information through these loops allows it to be maintained over time, and short-term memory capacity is determined by the "cycle speed," or the amount of information that can be successively cycled through each loop.

Long Term Memory. Finally, the entire diagram rests above the base of one massive arrow that folds back on itself: this represents long-term memory. Long-term memory has an essentially unlimited capacity, as indicated by this arrow's enormous base width, but is subject to decay and interference over time. Items can be retrieved from long-term memory, at which point a "gating function" permits us to actively think about the past (i.e., rehearse it), or to merely let it recur and disappear again from our "mind's eye." Note that:

• No arrow leads directly to long-term memory; one can only rehearse items and hope that this rehearsal process gives the memory long enough to seep into long-term memory.
• All processing beyond the sensory memory rests "on top" of long term memory representations. This illustrates an important aspect of working memory: everything we consciously perceive is placed within the context of those things we remember happening previously.

In conclusion, I hope that this model provides an intuitive way of visualizing how synchronized oscillations within cortical circuits may play a role in cognitive functionl, but please be sure to visit this post at Zero Brane for an alternative view on working memory.

Related Posts:

Working Memory: A Black Box? [Zero Brane]
Models of Active Maintenance of Oscillation
Functional Anatomy of Visual Short Term Memory
An Informal Integration of Object Recognition Models
Perceptual Sampling: The Wagon Wheel Illusion

PS, If you liked this, don't forget to digg it.

Towards a Cognitive Neuroscience of Intelligence

Kevin over at Intelligence Testing blog has found a really nice article on the relationship of traditional intelligence measures and some of the constructs more commonly used in cognitive psychology, such as working memory and executive function. The paper even goes into some neuroscience related evidence, such as the "neural efficiency" hypothesis and some interesting challenges that fMRI imaging is posing to both cognitive and psychometric approaches to intelligence testing.

Autoencoding Developmental Change in Vision

The human visual system begins essentially as a "blank slate," with only architectural connections, specific distributions of neuron types, and only the most basic of visual preferences specified at birth (not coincidentally, a preference for faces).

One of the hypothesized developmental changes in vision takes the form of the "representational acuity hypothesis," by Westermann and Mareschal. According to this view, neural receptive fields narrow in size based on experience; this perspective enjoys correlational evidence from infants below the age of 6 months, who are better at discriminating the faces of non-human species than those older than 10 months. The perceptual representation of faces becomes tuned with experience.

Additional behavioral evidence for this developmental changes in visual feature processing comes from a task in which infants are exposed to animals varying along three features (body, tail, and feet), with each feature having one of three possible values (giraffe, cow, or elephant body; feathered, fluffy, or horse tail; webbed, clubbed, or hoofed feet). In experiment 1, every animal presented to the infants had a unique combination of features until they were no longe rinterested in the stimuli (habituation of looking time, a standard measure of familiarization). Then, the researchers showed them three new animals: one which the infants had seen previously, one which combined features from multiple different animals in the initial familiarization set, and one which had completely new features. While 4 month olds only "dishabituated" to the completely novel animal, 7 month olds also looked longer at the novel animal with features drawn from the familiarization set. This result suggests that 7 month olds, and not 4 month olds, represent and maintain the correlations between visual items - and therefore perform "relational processing." Subsequent experiments showed that 7 month olds are not as sensitive to specific correlations between features as 10 month olds, and that this difference is not merely an increased novelty preference among 10 month olds.

The authors implemented a demonstration of the "representational acuity account" of these "featural to relational" changes using a self-supervised autoencoding neural network model. Such networks have been used to model infant eye-gaze behaviors, in which looking time is determined by the sum of squared errors between the input pattern and the "reconstructed" or "autoencoded" output pattern; the more error, the longer the looking times. These researchers used a Gaussian activation function as opposed to the standard sigmoid, and only the hidden-to-output weights were modified during learning. Although previous models had successfully simulated the performance of infants on a looking-time task, they had used unrealistic "batch" training input. In contrast, the current model was trained on real cases in sequence, locally coded as the presence or absence of specific feature types.

This model, like the previous ones, successfully simulated 10 month old infant behavior. But, by gradually changing the size of the receptive fields in the hidden layer, the authors were also able to simulate the behavioral results seen in 7 and even in 4 month olds. This is taken as evidence that changes in receptive field size are a sufficient mechanism to explain the developmental shift from featural to relational visual processing.

However, as the researchers admit, this account is a kind of "cheat" - the exact mechanisms guiding receptive field size change were not explicitly modeled. They offer two possibilities: internally generated neural activity ("noise") may decrease receptive field size, or unrelated external events may cause the receptive fields to shrink.

The models motivate further predictions: 4 month olds may actually be capable of showing relational processing if the features are sufficiently distinct from one another. According to the authors, preliminary evidence from Younger's lab suggests that strongly contrasting colors can actually encourage this behavior among 4 month olds. Second, the transition between these behaviors may appear to be rapid, but is really the result of more gradual underlying representational change. As in competing memory systems accounts of task-switching, different representations may compete for dominance in attentional networks, and at crucial developmental breakpoints can show extreme sensitivity to relatively slight changes in salience.

Related Posts:
Functional Anatomy of Visual Short Term Memory
Task Switching in Prefrontal Cortex
Learning Like a Child
Eigenfaces
Tuned and Pruned: Synaesthesia

Constraints and Optimality

Sometimes early neurological or morphological constraints can actually have positive effects in the long term; for example, in the case of Elman's neural network model of language learning, initial limitations on active maintenance abilties actually resulted in better corpus learning relative to networks that were not initially constrained. It appears that the constraints on motor skills in human infants may actually be a very important part of our eventual mastery at controlling our own bodies.

Nearly half a century ago, Bernstein realized that human infants learn many motor movements (such as walking, or grasping) first by locking their joints, so as to constraint the number of degrees of freedom they have to work with. After practice, the degrees of freedom are iteratively unfrozen beginning with those joints farthest from the infants' center of gravity.

Lungarella and Berthouze modeled this developmental progression in a several autonomous robots, one of which is pictured at the start of this article. They were able to show that motor performance is better in those robots that are given progressive control over their degrees of freedom than in those robots which are allowed to use all available degrees of freedom from the start. This same pattern was observed for a variety of motor skills, including the pictured simulation of a "jolly jumper" in which infants learn to bounce. Developmental constraints, such as the number of available degrees of freedom, may be an important mechanism in the eventual emergence of optimal behaviors.

The developmental approach to robotics is relatively new and unexplored. For example, although there are developmental robotic implementations of basic motor skill learning (reaching, grasping, gazing) there are none of more complex motor skills, such as running, walking, or dancing. Those systems that are capable of bipedal motion have been explicitly designed for bipedal motion, as opposed to being designed to learn.

Given the difficulty in traditional techniques for programming bipedal motion, one wonders whether developmental approaches might be better for other "hard AI" problems as well. To quote Lungarella et al.: "the designer should not try to engineer ‘intelligence’ into the artificial system (in general an extremely hard problem); instead, he or she should try to endow the system with an appropriate set of basic mechanisms for the system to develop, learn and behave in a way that appears intelligent to an external observer."

Illusory Motion Reversal: Rivalry or Perceptual Sampling?

During a previous discussion of the wagon wheel illusion, I endorsed the perceptual sampling hypothesis put forth by Van Rullen et al. to explain the phenomenon of illusory motion reversals of spinning wheels under continuous illumination (try it here). An incredibly clever experiment reported in Vision Research suggests that this illusion is not due to discrete sampling of the visual stream by attentional mechanisms (similar to movie's frame rate) but is instead due to rivalry between competing visual representations.

By showing subjects the wagon wheel illusion under continuous illumination, Kline, Holcombe, and Eagleman replicated the "illusory motion reversals" which seemed to support the perceptual sampling hypothesis. However, they also did something special: they also required participants to also report the reversals occuring in the illusion's mirror image. The authors reasoned that if these "motion reversals" actually indicate perceptual sampling, the mirror image should be seen to reverse direction simultaneously. Accordingly, ratings of motion reversal in the illusion or its mirror image did not correspond (and this same effect was also found when the illusion and its mirror image are presented to the same hemifield), suggesting that another process may be at work.

However, this conclusion rests on some tenuous assumptions. First, illusory motion reversals should be synchronized only if the various regions of the visual field are sampled with uniform frequency - this is an interesting prediction, but is not likely to be true given the nature of signal processing and its tradeoffs in temporal/spatial resolution. Second, attention is known to modulate the number of illusory motion reversals; to my mind at least, this is the fact that really suggests the wagon wheel illusion reflects higher cognitive processes. Since participants are unlikely to be able to pay attention to a visual illusion and its mirror image simultaneously, the different effects found in this study could be due to attention factors, as opposed to perceptual rivalry.

Instead, these authors propose that the illusory motion reversals are caused by competing Reichardt detectors: detectors for the illusory direction could become spuriously activated through temporal aliasing, which "happens because S1 occupies the receptive field on the left and, soon after, S2 moves into the receptive field on the right. The detector has no way of knowing that S1 and S2 are different stimuli." This explanation can be criticized on the basis of two facts: first, no Reichardt detectors have ever been observed in the mammalian visual system, and second, such an explanation does not actually argue against "perceptual sampling" but just moves it into the realm of temporal aliasing by a Reichardt detector, as opposed to temporal aliasing at a cognitively higher level.

EDIT: I have just learned that the following paper makes many of these same points:

Rojas, D., Carmona-Fontaine, C., Lo´pez-Caldero´n, J., & Aboitiz, F. (2006). Do discreteness and rivalry coexist in illusory motion reversals? Vision Research, 46(6–7), 1155–1157.

Related Posts:
Perceptual Sampling: The Wagon Wheel Illusion

Binding through Synchrony: Proof from Developmental Robotics

Neural synchrony is known to occur in a variety of contexts. For example, increased gamma band synchrony has been associated with focused attention and improved visual target detection, whereas gamma band synchrony decreases during the attentional blink. There's even some degree of causal, as opposed to purely correlational evidence: it appears the some brain rhythms can be entrained by external stimuli, which has direct effects on both visual binding and working memory functions. Thus, the importance of synchrony is well established in the recent cognitive neuroscience literature.

In contrast, the precise role of synchrony is still a matter of much debate. Although some have proposed a link between working memory capacity limitations and multiplexed synchronous gamma- and theta-band activity, others resist the idea. The skeptics believe that biological networks lack the temporal precision required to maintain multiple simultaneous synchronous states in polyphase. In their view, neural synchrony is also too transient to reliably encode anything, so it must simply be a byproduct of more important neural mechanisms.

This debate could be informed by some recent evidence from developmental robotics research in Gerald Edelman's lab at the Neurosciences Institute. In "Visual Binding Through Reentrant Connectivity and Dynamic Synchronization", authors Seth, McKinstry, Edelman and Krichmar have designed and implemented a biologically-plausible neural network architecture in a Darwin VIII robot.

The details of the implementation are as follows: the physical anatomy of Darwin VIII includes a CCD camera for vision, microphones for audition, infrared detectors for navigation, effectors for movement, and a 12 unit Beowulf cluster for the number crunching. Darwin's synthetic neuroanatomy consists of more than 53,000 units and over 1.5 million synaptic connections, with layers corresponding to V1, V2, V4, inferotemporal cortex (IT), superior colliculus, and ventral tegmental area (including a dopamine-like neuromodulatory system, based on an algorithm similar to temporal differences). For simplicity, the primary visual layer responds preferentially to green, red, horizontal, vertical and diagonal lines; all subsequent visual layers are bidirectionally connected and have increasingly large receptive fields (until IT, in which representation is non-topographic). The robot's orientation is guided by a topographic activity map in the superior colliculus layer, which also receives direct excitatory input from tones with specific amplitude and frequency picked up by the stereo microphones (this represents an a priori drive or bias for "target tones"). The dopamine system modulates synaptic efficacy between itself and IT, as well as between IT and superior colliculus, with effects that last several processing cycles. All areas contain both recurrent excitatory connections and lateral inhibition.

Neural activity was modeled via a mean firing rate model, with one small addition: a phase parameter "provides temporal specificity without incurring the computational costs associated with modeling of the spiking activity of individual neurons in real-time." All synaptic connections were modeled as phase-dependent, such that new phases are chosen at random unless the a unit's presynaptic input phases surpass a threshold, after which phase changes are first sent through a nonlinear "squashing" function and then scaled by a phase learning rate. This implementation causes postsynaptic phase to be influenced in the direction of the most active presynaptic units' phases. Synaptic efficacy is modified both with traditional firing-rate dependent credit/blame assignment, as well as with phase-dependent credit/blame assignment, in which units with tightly coupled phases are subject to potentiation, and those with uncoupled phases are subject to depression.

The experiment was divided into training and testing phases; during training, Darwin autonomously explored an environment consisting of one target item and three distractor items which share multiple attributes with the target item. For example, if a red diamond was the target, red squares and green diamonds would be distractor items. At the beginning of each training phase (which was repeated for three different Darwin "subjects"), all weights were randomized. Throughout the training phases, sounds were emitted from speakers which caused Darwin to orient towards the target. In the testing phase, these speakers are turned off and Darwin is allowed to explore its environment for another 15,000 cycles.

The authors measured Darwin's ability to locate the targets in its environment: each simulated subject was able to do so over 80% of the time. As the authors point out, " It should be noted that successful performance on this task is not trivial. Targets and distracters appeared in the visual field at many different scales and at many different positions as Darwin VIII explored its environment. Moreover, because of shared properties, targets cannot be reliably distinguished from distracters on the basis of color or shape alone."

At each timestep in the experiment, the researchers took a "snapshot" of the activity in every unit, and the weight of every connection. Results showed self-synchronization among neurons with recurrent connections within only 15 cycles; when reentrant connections were lesioned, no synchrony occurred within 10,000 cycles. Most importantly, multiple simultaneous synchronous firing patterns were observed within the active units of both IT, superior colliculus, and the value system (dopamine) layer, with both more synchrony and higher firing rates in circuits corresponding to targets or target features; in their own words, "the simultaneous viewing of two objects clearly evoked two distinct sets of circuits that were distributed throughout the simulated nervous system and distinguished by differences in the relative timing of their activity." In other words, multiple polyphase patterns of synchronous firing can self-organize inside a network with the proper architecture and environment.

The authors emphasize that their model should not be taken as evidence that highly regular brain oscillations at any specific frequency are essential to binding, but simply that synchronous activity at some frequency is important to binding. However, given the previous research on the role in gamma-band synchrony, it is self-evident from their model that binding limitations would be directly related to the number of distinct synchronous firing patterns that can exist out of phase with each other (as hypothesized previously).

Related Posts:
Models of Active Maintenance as Oscillation
Functional Anatomy of Visual Short Term Memory
An Informal Integration of Object Recognition Models
Perceptual Sampling: The Wagon Wheel Illusion